SUDOKU joc d’ intuïció i de deducció
NOMENCLATURA
Sudoku és el nom que rep un joc provinent del japó i que consisteix en omplir una graella de vuitanta-un quadrats (9×9) amb números de l’u al nou, de manera que no es repeteixin, dins d’uns àmbits que anomenarem grups, i poden ser columnes, files i regions.
La fila la constitueixen el conjunt de nou quadrats en direcció horitzontal.
La columna els nou quadrats en vertical.
I la regió el conjunt de nou quadrats en format de 3×3. Per entendre’ns podem batejar les regions com a Primera, Segona, Tercera, etc, començant per la superior esquerra i acabant per la inferior dreta. Així la del mig serà la cinquena.
També per identificar les cel·les amb precisió, podem utilitzar la nomenclatura dels escacs i numerar les columnes amb lletres de l’abecedari de la a fins a la i d’esquerra a dreta, i les files amb números de l’1 fins al 9 començant per la part superior de la quadrícula.
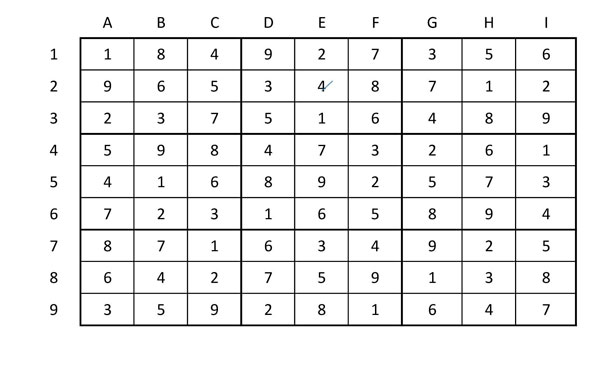
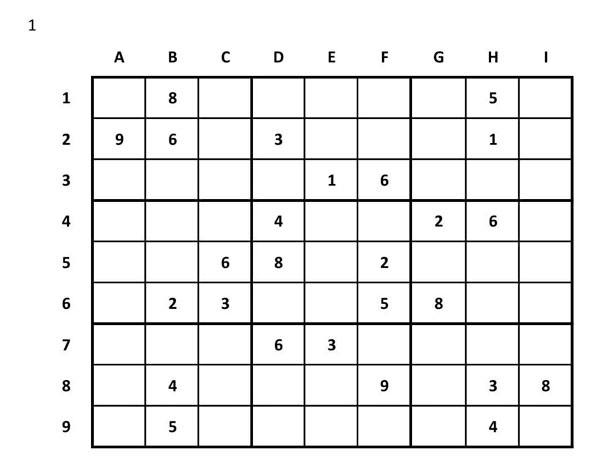
Així en el requadre de sota, el número 1 està a la cel·la B2 (primera regió), el número 2 està a la D5 (cinquena regió) i el número 3 a la I9 (novena regió)
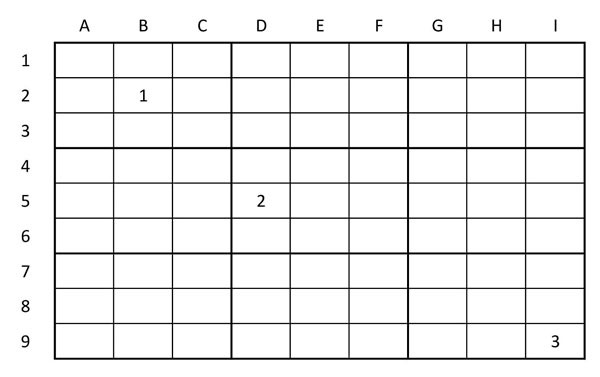
Els Sudokus vénen presentats amb alguns números ja donats, i nosaltres haurem de complementar les caselles buides de manera que no es repeteixin ni en horitzontal, ni en vertical, ni dins de les regions. D’entrada sembla molt senzill, però en realitat hi ha diferents nivells de dificultat que no sempre acostumen a coincidir amb la quantitat de números que ens mostrin d’entrada. I la complexitat pot anar creixent fins a nivells pràcticament irresolubles.
SOLUCIÓ DE SUDOKUS – SUDOKU SENZILL
Ara iniciarem pas a pas la resolució d’un Sudoku senzill.
Per començar, l’escanejar és la manera inicial, i constant, de resoldre els sudokus. Es tracta de passar la vista al llarg d’una filera, o d’una columna, o d’una regió i descobrir quin és el número que només pot anar a una casella. Aquesta és la manera de començar tots els sudokus, perquè és l’única que ens il·luminarà les possibles solucions als que no tinguem coneixements matemàtics avançats ni siguem experts en algoritmes.
1.- He triat un Sudoku molt senzill a fi de poder seguir pas a pas aquest procés. Sudoku original
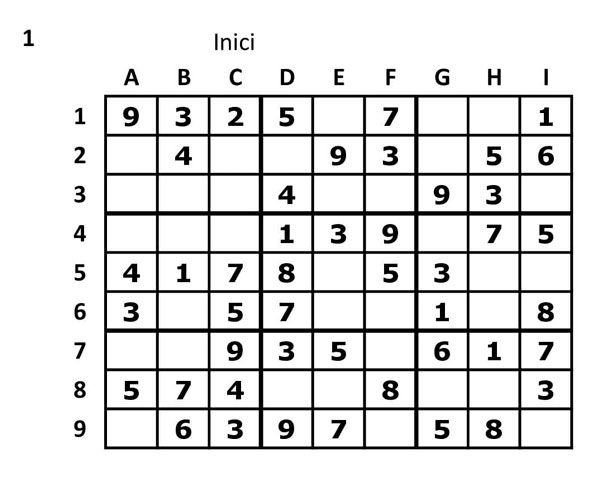
2.- Primer procedirem a escanejar les regions (Conjunt de nou cel·les en format 3 x 3), començant per la primera i analitzant quins números podem posar a cada casella. Conforme anirem agafant pràctica veurem que a vegades apliques varis sistemes d’escanejar a la vegada (analitzes per regions i per columnes i per files a la vegada). Jo, per fer-ho pas a pas m’he limitat a fer exclusivament el de cada pas, o sigui, ara el de les regions. Quedaria així:
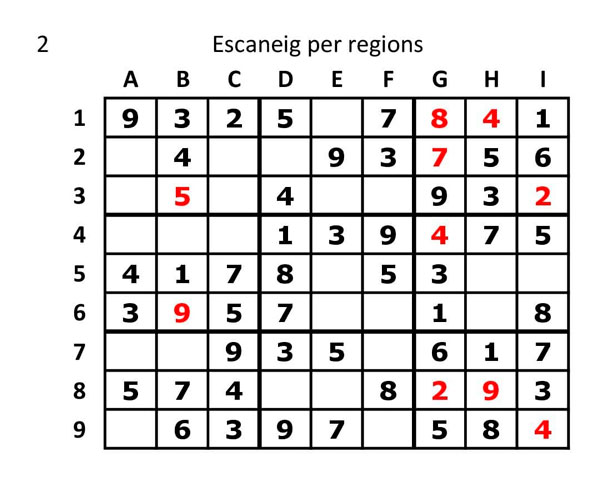
3.- Escanejar per files (Conjunt de nou cel·les en posició horitzontal, des de la A fins a la I): Repeteixo el que ha dit abans: només em limito a posar un número quan cal a la fila, encara que vegi que per c0lumnes en podria posar algun altre. Ja arribarà.
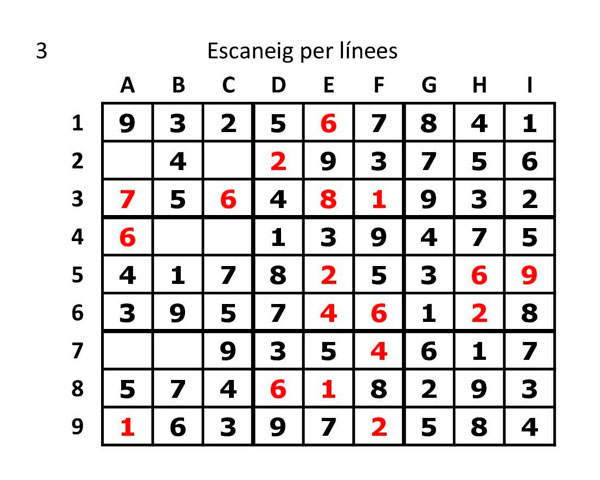
4.- Escaneig per columnes (Conjunt de nou cel·les en posició vertical, des de l’ 1 fins al 9):
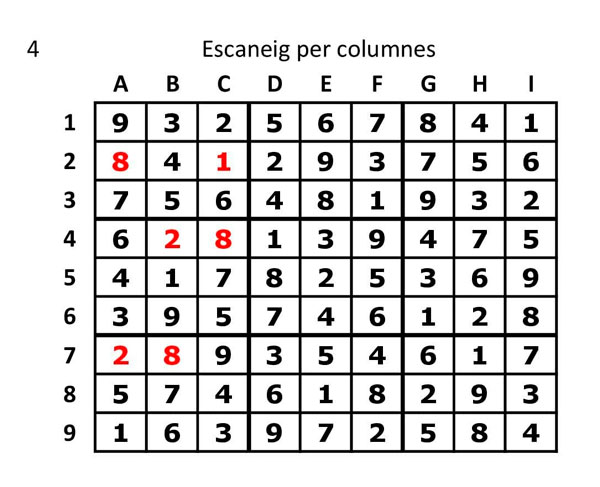
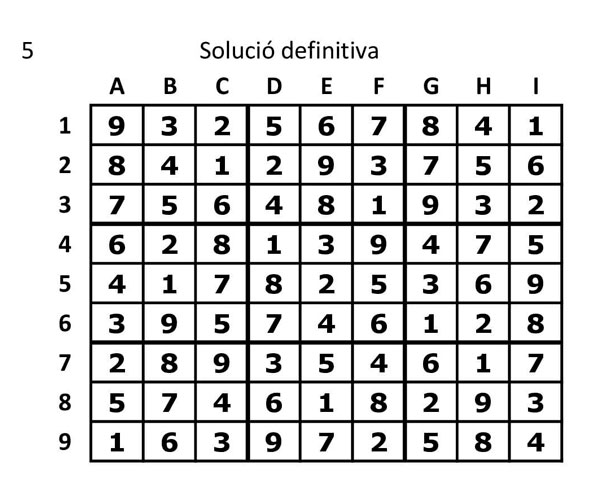
5.- Sudoku resolt. Ja hem omplert totes les cel·les. Queda així
TÈCNIQUES DE RESOLUCIÓ DE SUDOKU – SEGON NIVELL
Els doblets
Quan ja haguem situat tots els números únics als seus llocs no ens quedarà altra remei que omplir la resta de caselles amb els números candidats. Així veurem que a una casella concreta hi pot optar el número 3, el 6 i el 7, per exemple. Els escriurem ben petitons perquè càpiguen a la casella (com que conforme anem avançant n’haurem d’esborrar alguns d’aquests candidats, haurem de portar una goma d’esborrar si pot ser no gaire gruixuda). Anem per ordre:
1.- Sudoku original
 2.- Posarem totes els números que puguem posar escanejant:
2.- Posarem totes els números que puguem posar escanejant:
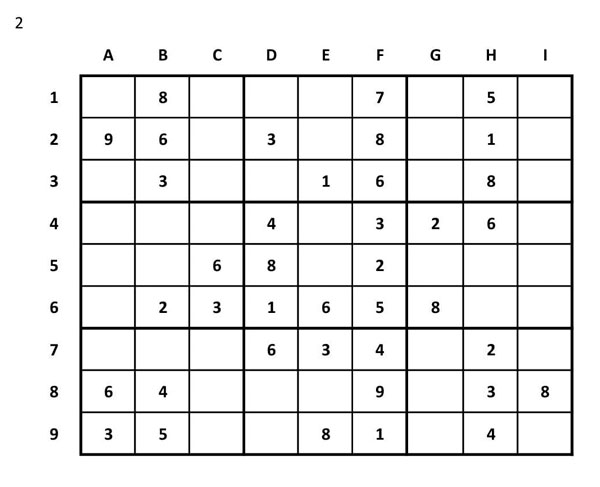
3.- Escriurem tots els números possibles a cada casella.
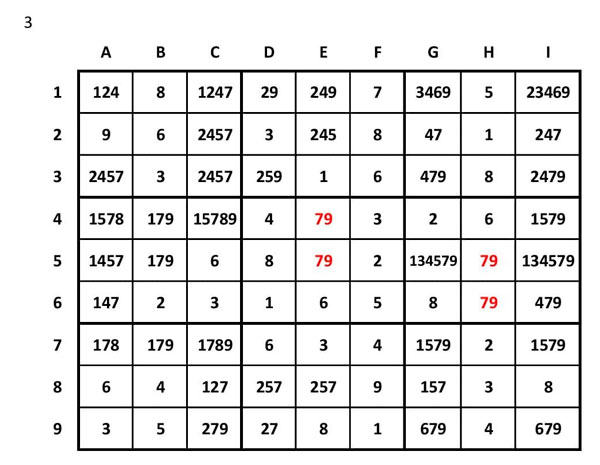
4rt.- Parelles dobles (o doblets):
Ara ha arribat l’hora d’aplicar tècniques més avançades de solució de Sudokus. Per exemple, si en algun dels tres conjunts (fila, columna o regió) hi ha dues caselles amb dues xifres úniques i repetides, deduirem que aquests dos números només poden anar en alguna de les dues caselles, i si n’hi ha a d’altres caselles del mateix grup els podrem eliminar.
Veiem que a la fila 5 hi ha dues cel·les amb els números 7 i 9. Com que el 7 i el 9 hauran d’anar obligatòriament a cadascuna de les dues caselles, podrem eliminar el 7 i el 9 de les altres cel·les del seu grup (en aquest cas de la fila 5)
També hi ha dues cel·les amb els números 7 i 9 a la columna E, i podrem eliminar aquests aquests números de les altres cel·les de la columna.
I també hi ha els números 7 i 9 a la regió 6, hi podrem eliminat aquests números d’aquesta regió (cel·les G5, I4, I5 i I6).
D’aquestes situacions de dues cel·les amb dos números iguals a cada cel·la se’n diuen doblets.
5.- Un cop depurades totes aquestes cel·les quedaria així:
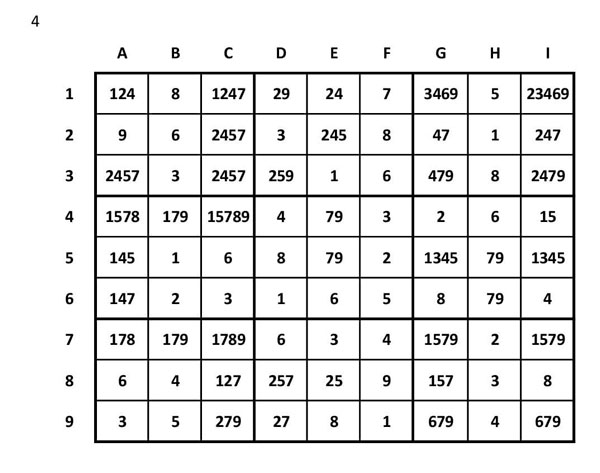
Veieu que a la cel·la B5 ha quedat un candidat únic, el número 1, que ens permetrà depurar unes quantes cel·les més. I també a la I6 també hi ha quedat un sol número, el 4, que també ens permetrà fer una mica més de neteja.
Campionat de Sudoku a Caldes de Montbui

Números exclusius al Sudoku
Hi ha altres mètodes d’eliminació de candidats. Imagina’t que analitzes una fila o una columna. La fila o la columna travessa tres regions. Si hi ha alguns números de la fila o columna que només estan dins d’una regió, per exemple el número 2 de la regió 7 columna C (cel·les B8 i B9) deduireu que el número 2 només pot anar en aquestes cel·les d’aquesta regió ja que no n’hi ha cap més. 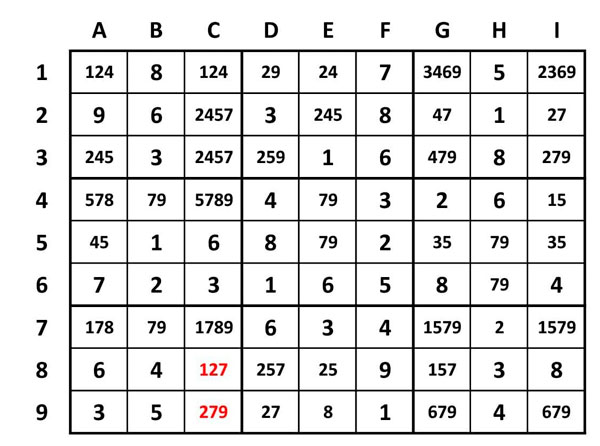
Per tant, els números 2 de la primera regió de la columna C (cel·les C1, C2 i C3) els podrem eliminar. Quedaria així:
Hi ha altres posicions que ens donen llum quan la cosa està espessa, però ja n’anirem parlant sobre la marxa. A tall d’enunciat us diré que també hi ha triplets, quan a una regió hi ha tres números iguals o estretament vinculats, per exemple: 12, 23, 123 en que l’1, el 2 i el 3 aniran sempre a alguna de les tres caselles. En direm triplets i funcionen exactament igual que els doblets.
Altres tècniques són l’ X-Wind (que es diu així perquè els números juguen formant una X) i el Swordfish, que ve a dir que connectant diverses cel·les pretenem “pescar” algun número d’una altra cel·la. Els menciono, tot i que aniran sortint en exemples posteriors.
X-Wing (Números en X)
L’X-Wing és una tècnica avançada que juga amb un número o dos d’iguals que queden afectats per una sèrie de rebots. Imagineu-vos que a una casella només hi pot anar l’1 o el 2. Diem: i si hi va l’1? Llavors ens adonem que aquesta decisió modifica una altra casella que està en una altra regió de la mateixa fila, i que a la vegada, aquesta modificació afecta a una altra casella que està a la mateixa columna de la segona casella modificada, i aquesta darrera cel·la afecta de rebot una altra cel·la que està a la mateixa fila de la darrera cel·la modificada (això passa sovint). Fins ara aquests raonament no porten enlloc, però a vegades tant si escollim un número com un altre, ens trobem que sempre afecten de la mateixa manera a una altra casella (en la imatge següent afecta al número 1)
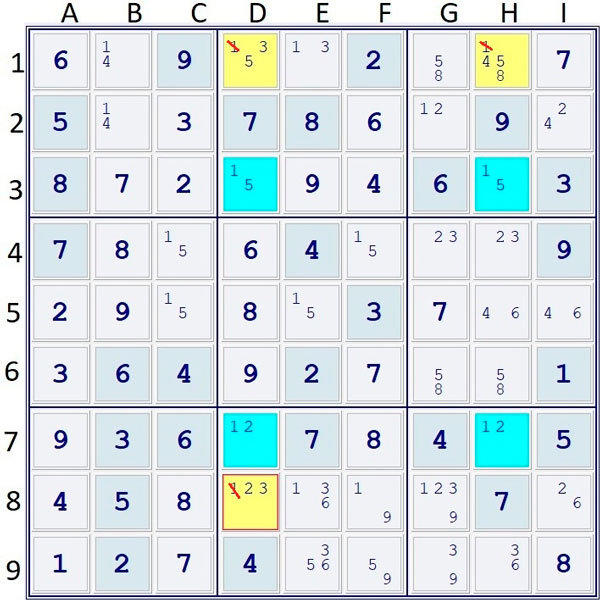
L’X-Wing pren aquest nom perquè si prenem una decisió en una casella té efecte en una altra que està en diagonal, i si prenem la decisió contrària també afecta a un altre que està en diagonal. I quan es creuen formen la lletra X. Però la virtut és que a vegades aquests resultats afecten d’igual manera a una tercera cel·la.
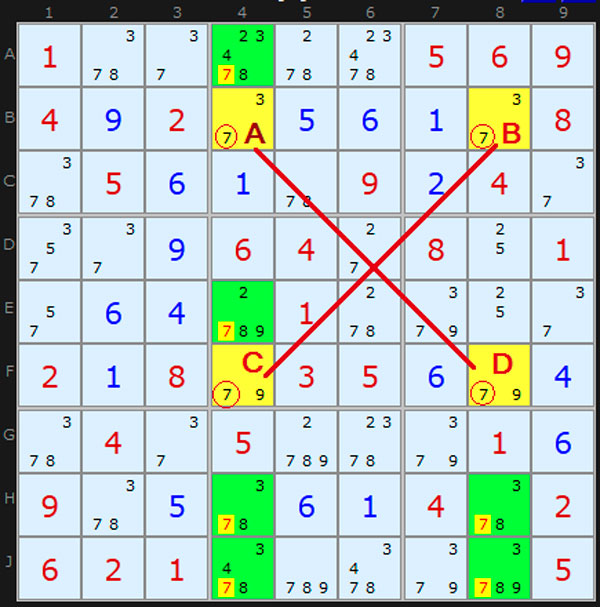
L’Swordfish (o la tècnica del pescador)
El Swordfish ve a ser un X-Wind en el que hi intervenen un mínim de tres files, i també al final queda afectada alguna casella, sempre de la mateixa manera, que no està en aquest recorregut.
Em sembla que per avui ja n’hi ha prou. Si has pogut entendre el que volia explicar, suposo que desitjaràs començar a resoldre algun sudoku d’aquells que en diuen difícils i inclús “per experts”. No sé si algun dia coincidirem en algun dels concursos del país, però només per la il·lusió que fa quan els resols ja haurà valgut la pena.
Aleix Font, 9 d’abril de 2021
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MECÀNICA DELS SUDOKUS
Us explicaré com faig els Sudokus. Hi ha gent d’una ment privilegiada que només amb una mirada van veient on situar els números a les seves cel·les correctes. Efectuen, tal com ho faig jo, un escaneig a dins dels blocs (files, columnes, regions) i van veient on queden les cel·les amb candidats únics. Però jo no arribo a tant i ho faig per etapes.
1.- Escanejar les regions: on pot anar un número concret sense que n’hi vagi cap altre. Començo per l’1, després el 2 etc.
2.- Escanejar les files. On hi va només l’1, on només el 2, on només el 3….
3.- Escanejar columnes. El mateix d’abans.
Comencem per ordre
Sudoku en origen
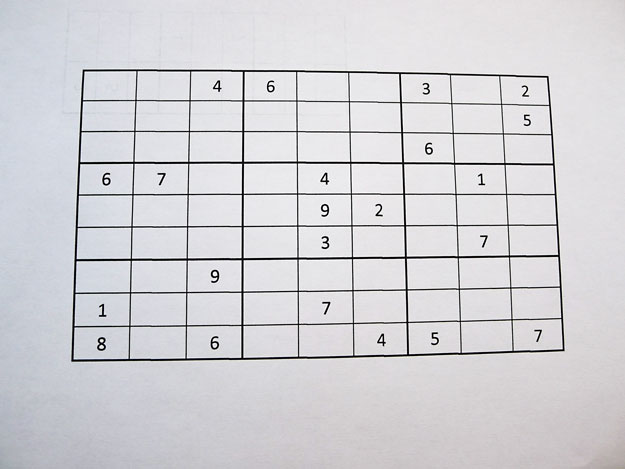
Començo per escanejar els números 7, perquè em fa l’efecte que n’hi ha més. Després els aniré mirant tots per ordre, l’1, el 2, el 3.. fins al 9. I tornaré a començar, perquè si n’he posat alguns pot haver propiciat noves cel·les exclusives (amb només un candidat) Quedaria així:
Candidats únics
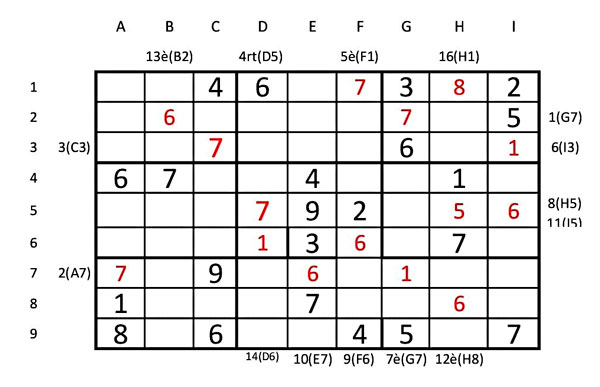
Als costats hi veureu l’ordre en que he anat situant els números. Primer els 7 (G2, A7 C3, D5, F1. Després els 1: I3, G7. Com que no puc situar cap 3 ni 4 ni 5, continuo amb els 6: H5, F6, B2. El 8 només a H1, i de 9 no en veig cap. Per tant començarem amb la següent fase.
Ara escriurem tots els números candidats a cada cel·la:
Tots els candidats possibles
Ara escriurem tots els números candidats a cada cel·la:
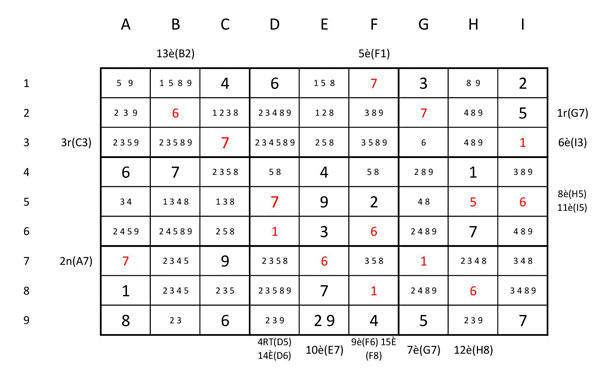
Comença la depuració de números. Jo sempre començo, si és possible amb els blocs on hi hagi dues cel·les amb dos únics números iguals.
A la fila 4 (comença amb el número 6) hi trobareu dos números 5 i 8 (cel·la D4 i F4). Si a una d’elles hi va el 5, a l’altra hi anirà el 8. Per tant tots els 5 i 8 de les altres cel·les de la fila es poden eliminar: Cel·la C4 (de 2358 passa a 23), G4 (de 289 passa a 29) i I4 passa de 389 a 39.
També es podrien eliminar els 5 i 8 de la seva regió, però en aquest cas no n’hi ha cap.
Continuem amb números únics a cada bloc.
A la columna H, a la regió de dalt hi ha tres números que són exclusius d’aquesta regió, el 4 el 8 i el 9. Si a una cel·la hi va el 4, a una altra hi anirà el 8 i a l’altre el 9. Per tal no poden anar a cap altre cel·la de la columna. Cel·la H7 (De 2348 passarà 23. H9 (de 239 passarà a 23).
A la regió no hi ha altre cel·les disponibles. I les files no constitueixen un bloc.
A la regió 9 (a baix a la dreta) a la columna H han quedat el número 23 a dues cel·les (H7 i H9). Només poden anar a aquestes cel·les d’aquesta columna. Per tal podem eliminar tots els altres 2 i 3 d’aquesta regió:
Cel·la G8 (De 2489 passa a 489), Cel·la I7 (de 348 a 48), cel·la I8 (de 3489 a 489)
Amb aquest procés ens ha deixat a la cel·la I4 un únic candidat, el 3 (no pot anar enlloc més de la columna). I per tal eliminarem el 3 de la cel·la C4 (De 23 passarà a 2, únic candidat. I aquest 2 ens dóna un únic candidat a la cel·la G4, el 9.
Ara hem de netejar tots els números dels seus blocs: Columna C: C2 (1238 a 138), C6 (258 a 58), C8 (de 235 a 35), Regió 4: Cel·la A6 (2459 a 459) B6 (24589 a 4589).
Columna G: G6 (2489 a 248) i G8 (de 2489 a 248). I també a la I6 (489 a 48). Ens ha quedat un únic 2 a la regió 6, cel·la G6.
I també a la regió 9, hi ha dues cel·les amb el 48, o sigui que a una hi anirà el 4 i a l’altra el 8. Per tal podem eliminar el 8 de la cel·la I8 i hi queda un únic candidat de la columna, el 9 cosa que eliminarà el 9 de la cel·la D8 (23589 a 2358)
A la regió 7(a baix a l’esquerra) veiem que els 2 només poden anar columna B. Per tal l’eliminem de B3 (23589 a 3589).
Igualment a la columna B, els números 4 només poden anar a la regió 7. Per tal eliminarem els de la cel·la B6 (de 4589 a 589), B5 (1348 a 138)
A la columna F només hi ha un únic 1 (F2), i elimina el de E1 (158 a 58), E2 (de 128 a 28) i C2 (138 a 38)
A la columna F només hi ha un únic candidat pel 9 a F3, i elimina els 9 de: A3 (de 2359 a 235), B3 (de 3589 a 358), D2 (23489 a 2348) D3 (234589 a 23458) i de H3 (489 a 48)
A la columna C hi ha un únic candidat per l’ 1 a C5 i elimina el de B5 (138 a 38)
A la columna B hi ha un únic candidat per l’ 1 a B1
A la cel·la B6 hi ha l’únic candidat al 9 i elimina el de A6 (459 a 45).
Primer escaneig
I momentàniament quedarà així:
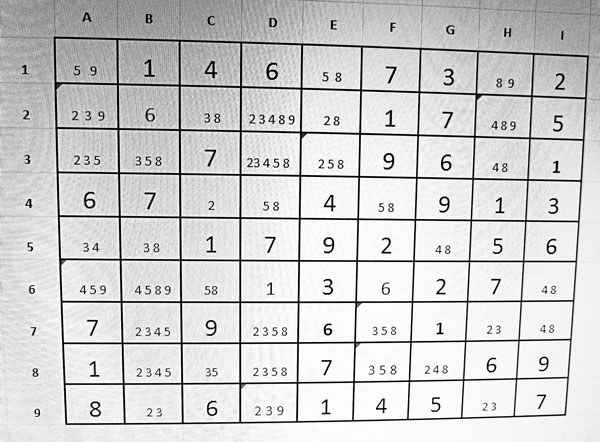
A partir d’ara ja no hi ha possibilitats de solucions per escaneig i caldrà aplicar tècniques superiors.
A la regió 2 a la columna E hi ha a E1 58, E2 28 i a E3 258. Totes les tres cel·les formen un conjunt de números exclusius ja que obligatòriament el 2 el 5 i el 8 aniran a una d’aquestes tres cel·les (proveu de fer combinacions). Per tant, la cel·la D2 (de 23489 a 349) i la D3 ( de 23458 a 34)
A la columna D han quedat dues cel·les amb dos números iguals, cosa que exclou els mateixos de la columna. E7 (2358 a 258), E8 (2358 a 258) i E9 (239 a 29)
Ara a la fila 9 hi ha dos números iguals el 23 a B9 i a H9. O sigui que podem treure el 2 de E9 i ens queda un candidat únic a E9, el 9
A la columna B, a B6 hi ha un candidat únic amb el 9. I elimina el de A6 (459 a 45)
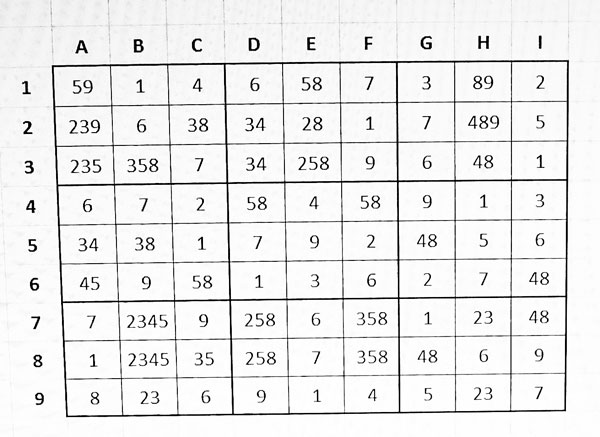
I ara hem arribat a una situació molt difícil, pràcticament irresoluble si no trobem una combinació guanyadora. I només n’hi ha una que vindrà per dues possibilitats. Tenint en compte que a la regió 6 hi ha dues úniques cel·les que tenen 48 Suposem:
1, I6=8, C6 =5, A6=4 i A5=3– Això pressuposa que ni A2 ni A3 poden tenir el 3
Si I6=4, A6=5, C6=8 i C2=3. Això pressuposa que ni A2 ni A3 poden tenir el 3, i per tant, a la columna A5=3
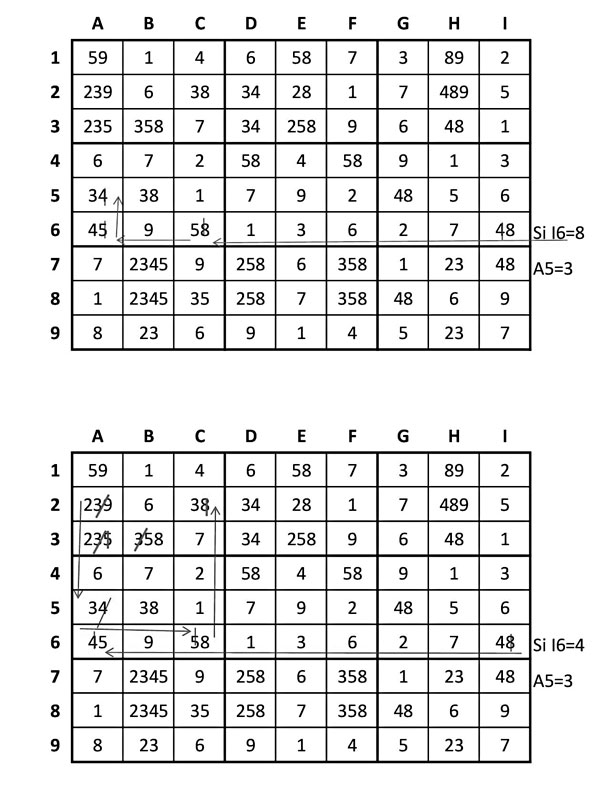
Però si ni A2 ni A3 poden portar el 3 en els dos casos, el 3 necessàriament ha d’anar a A5. O sigui que l’opció correcte és I6=8
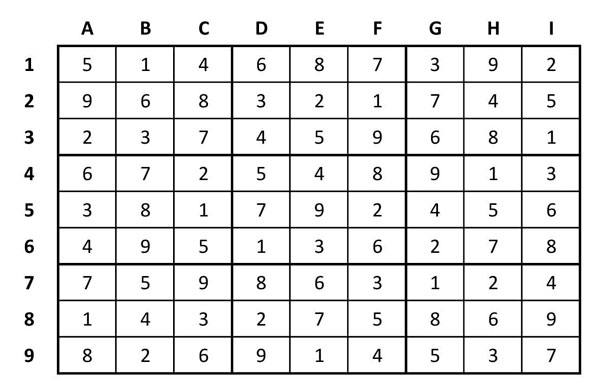
Per tant: I6=8, C2=8, A6=4, A5=3, B5=8 i etcètera. Ara van caient tots fins que acabarà així:
&&&&&&&&&&&&&&&&&&&&&&&&&&
HI HA MOMENTS EN QUÈ CAL ESCOLLIR
SUDOKU AMB RESOLUCIÓ PER TAMPTEIG: “I si….?”
Tècnica Nishio
El Sudoku inicial. Desconec com s’ho fan els dibuixants de sudokus per saber d’entrada quins són els fàcils i quins els difícils. Perquè a vegades, la quantitat de números exposats són els mateixos en uns que en altres. I alguns dels difícils són realment difícils, tant que podríem dir que no tenen una solució diàfana i hem de recórrer al discerniment de probabilitats.
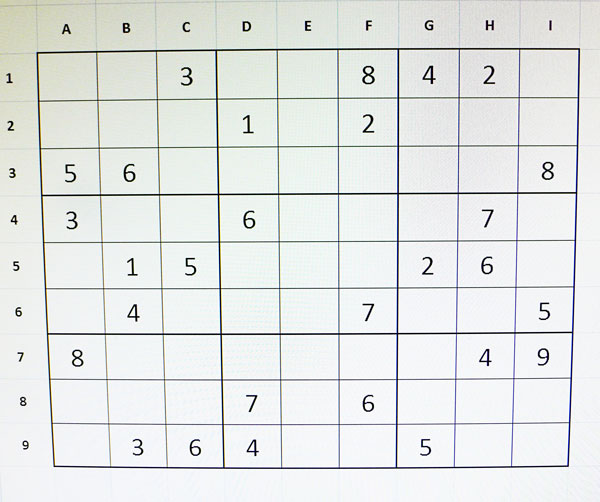
El primer pas és omplir totes les cel·les que es puguin a primera vista. Amb les cel·les de candidat únic plenes. Ja tenim 41 números col·locats i tot augura que la resolució pot ser senzilla.
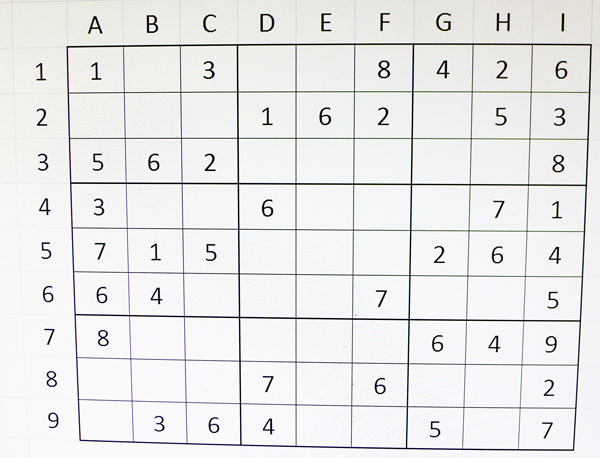
Ara posarem tots els números possibles a cada casella buida.
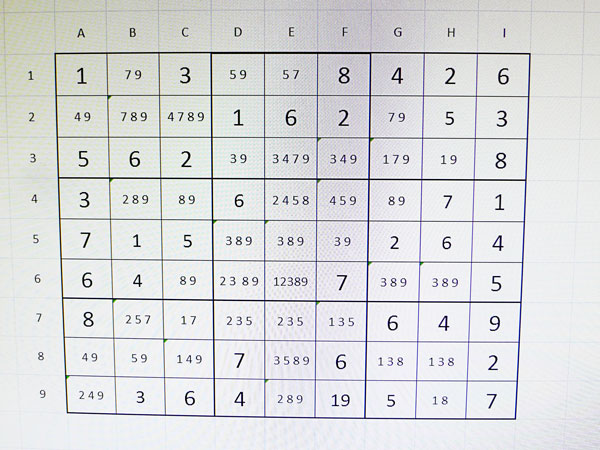
Ara és el moment d’0bservar i començar a prendre decisions. Inici d’especulacions:
Doblet: Columna A, cel·la A2 i A8 amb parella idèntica (49). Per tal a A9 podem eliminar el 4 i el 9. Queda només el 2. Podem treure els dosos de la regió (B7, de 257 passa a 57). També podem treure els de la fila (E9, de 289 passa a 89).
Doblet: Columna C, cel·la C4 i C6 hi ha dos números iguals, el 8 i el 9. Podem eliminar tots els de la columna que portin 8 o 9. (C2 passa de 4789 a 47), (C8 passa de 149 a 14). A la fila 2 només hi ha quedat un 8, a B2.
Doblet: Fila 4. Hi ha dues cel·les, C4 i G4 amb dues parelles idèntiques, 8 i 9. Podem eliminar aquests números de la fila. (E4, de 4589 a 45) (F4, de 459 a 45).
A la Columna B només hi ha un dos a B4. Podem eliminar el dos a E4 (queda 458).
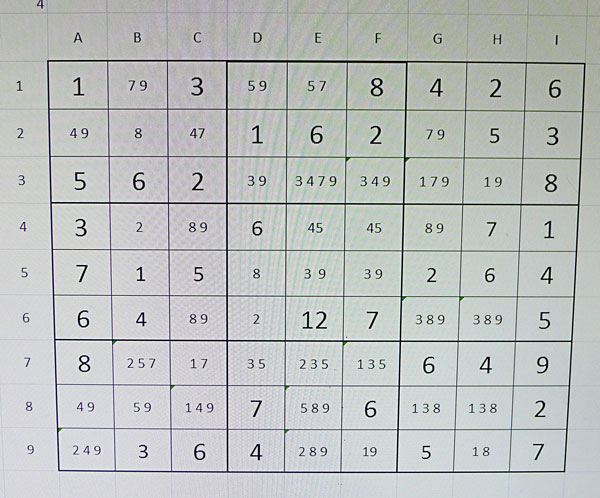
Ara quedaria com la imatge 4 i comença el procés d’especulació (Tècnica Nishio):
Fila 6: cel·la C6=89, Cel·la G6=389, Cel·la H6=389.
Si C6=8, G6 i H6 =39 (i quedaren dues parelles iguals.
Si C6=9, G6 i H6 =38 (i quedaran dues parelles iguals. O sigui, que els 3, 8 i 9 es poden eliminar de la fila: (D6, de 23589 passa a 2 I el 2 és número únic a la fila, i (D7 passa de 235 a 35). I l’1 d’E6 és número únic a la fila.
Regió 9; Cel·la G8=138, Cel·la H8=138, Cel·la H9=18
Si H9=1, G8 i H8= 38
Si H9=8, G8 i H8=13.
És a dir, que el 3 sempre formarà part d’una parella. I per tal, el 3 es pot eliminar de la fila.
(E8, de 3589 passa a 589)
A la columna D només hi ha un 8 a D5. Per tant eliminem els 8 de la fila. Queden a E5 i F5 dos números iguals, el 3 i el 9
A les columnes E i F hi ha dues caselles amb dos números cadascuna (fila 5 i fila 9), i en totes quatre hi ha un número 9. És a dir, que el 9 sempre anirà a E5 o E9, o a F5 o F9. Per tant eliminem els 9 d’E3 i F3
També veiem que a E7 hi ha l’únic 2 de la columna.
I ara quedarà així:

Tinc el pressentiment que us passarà com a mi, que sembla irresoluble. Entrem en una fase d’aconseguir ni que sigui eliminar tan sols un número amb l’esperança que aquesta minsa victòria ens durà a desencallar alguna cosa.
Hi ha una figura en la resolució de Sudokus anomenada Tècnica X-Wind i que consisteix en lligar quatre cel·les de manera que al posar un número a una casella implica que el mateix número vagi al que està a la seva diagonal. I aquesta és la tècnica que intentarem aplicar.
Podríem tenir un X-Wind a les cel·les E5, F5 i E9 i F9, amb el número 9.
També en podríem tenir un a les cel·lesE5 i F5 i E3 i F3, amb el número 3.
El que vull intentar és que a la cel·la D3 només hi quedi el 9. I per això veig que a E3 i F3 hi ha el número 4 que és exclusiu d’aquestes dues cel·les. De manera que amb el X-Wind de la línea 5 ho forçaré. Veureu que l’operació no és neta i diàfana, però és l’única que he aconseguit després de moltes hores de calcular possibilitats. Comencem.
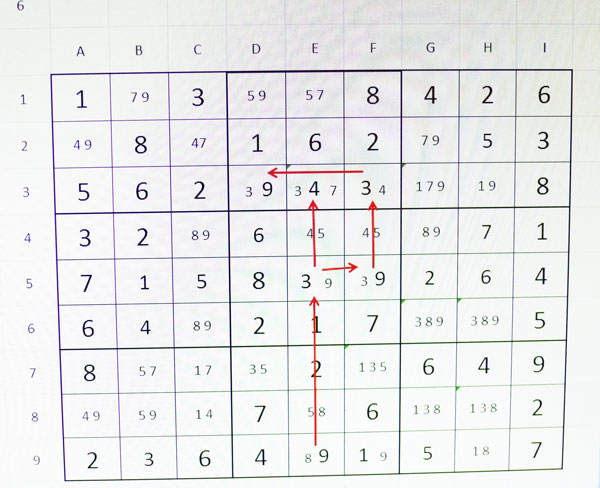
Si F9=9 implica que F5=3 i F3=4. A la vegada amb F5=3 implica que e5=9 implica queE3=3 i D3=9
Si E9=9, E5=3 , Per tan a E3 no hi ha el 3, per tant hi hauré de posar el 4 per mantenir la meva pretensió que el 3 i el 4 vagin a E3 i F3. En conseqüència el 3 anirà a F3 i a D3 hi queda també el 9. A partir d’aquí ja és una cadena d’eliminacions que ens durà fins a omplir tots les altres cel·les dels Sudoku quedant com a la figura 6.
Escollirem E9=9 perquè després de provar-ho he vist que tot anava bé sense cap duplicitat a les regions, a les línees i a les columnes. Si la combinació no hagués sigut correcte hi hauria hagut duplicitat de números en alguna regió. O sigui que podem dir que ho hem fet bé. Per tant, el resultat final és aquest:
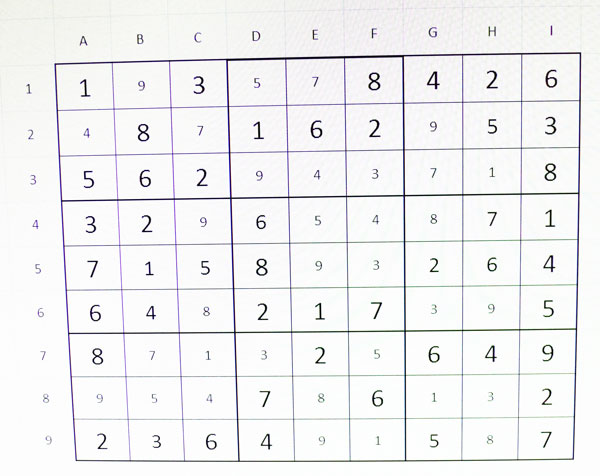
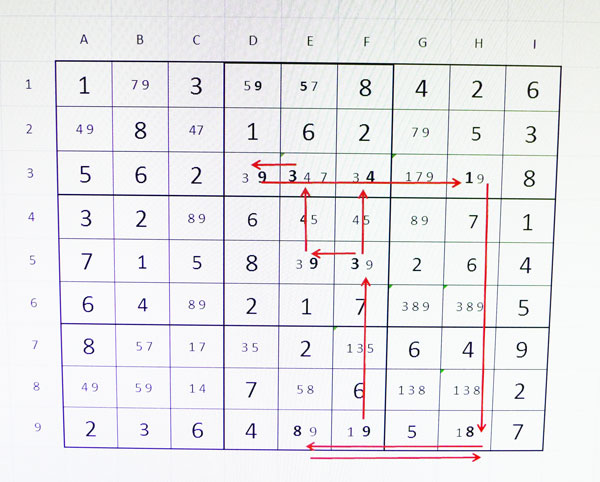
Què hauria passat si haguéssim pres l’altra opció? Provem-ho:
F9=9 implica que F5=3 implica que E5=9 implica que E3=3 implica que F3=4 implica que D3=9 implica que H3=1 implica que H9=8 que coincideix amb E9=8
Aleix Font, 6 de maig de 2021
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
Un altre exemple de Sudoku amb un final imaginatiu
Ara us explicaré com he fet aquest sudoku que té una dificultat a partir d’un moment en que no sembla haver-hi cap tria possible.
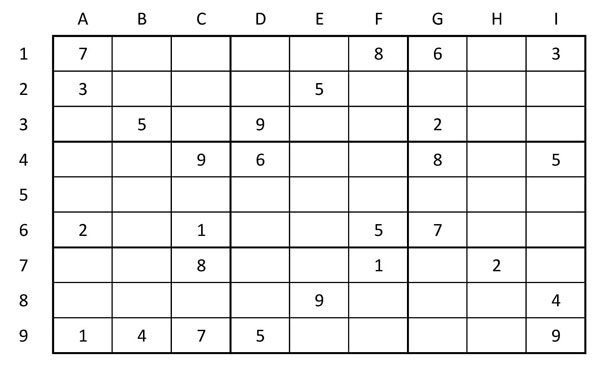
1.- Partim del Sudoku d’origen – 1
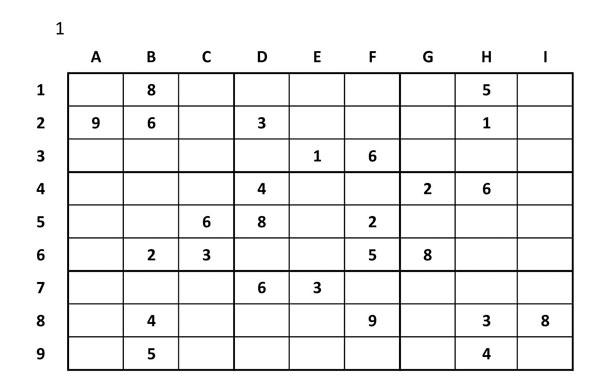
Ara caldrà escanejar tots els grups per determinats cel·les amb candidats únics
Memòria: Anomenem grups als conjunts de cel·les on hi aniran els números de l’1 al 9 sense repetir-los. O sigui, les columnes, les files i les regions.
A una columna hi ha les nou files, de la 1 fins a la 9
A una fila hi ha nou columnes, de la A fins a la I
A una regió hi haurà nou caselles en un quadrat de 3×3
Pas número 2
Omplim les cel·les amb candidats únics
Ara haurem d’escriure a cada casella tots els candidats possibles a primera vista. Això ens estalviarà feina pel següent pas.
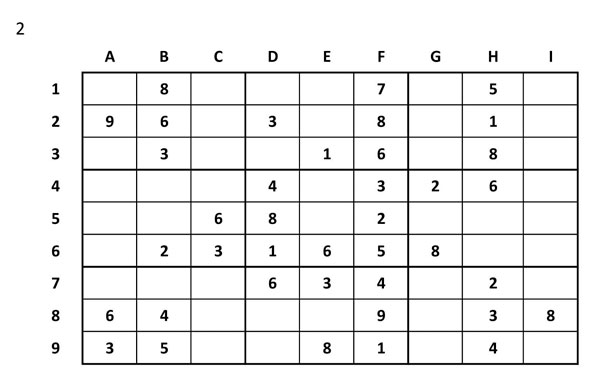
Pas número 3
Tots els candidats possibles
Escriurem a cada casella tots els números possibles que hi puguin anar, considerant que no n’hi pot haver cap que sigui repetit en algun grup que afecti la casella.
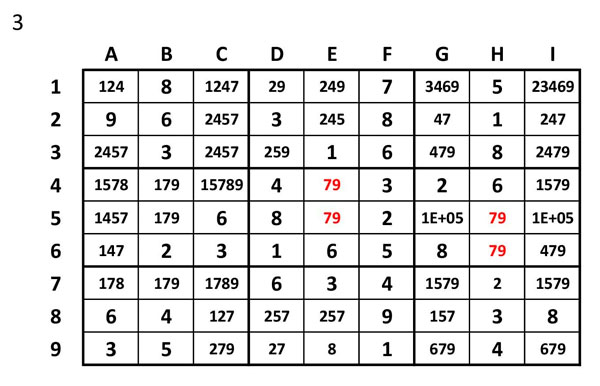
I un cop tot ple veiem que hi ha algunes caselles amb els mateixos números dobles.
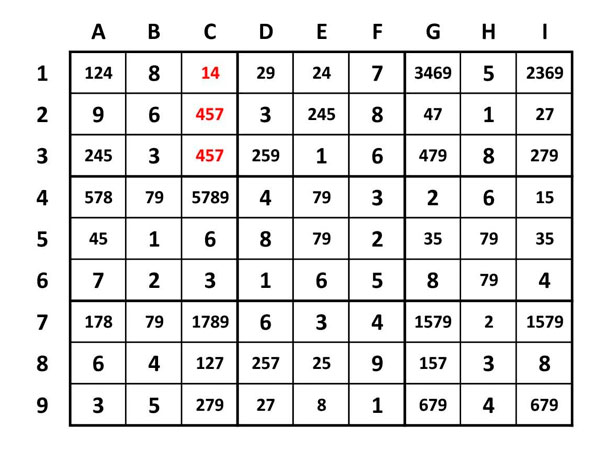
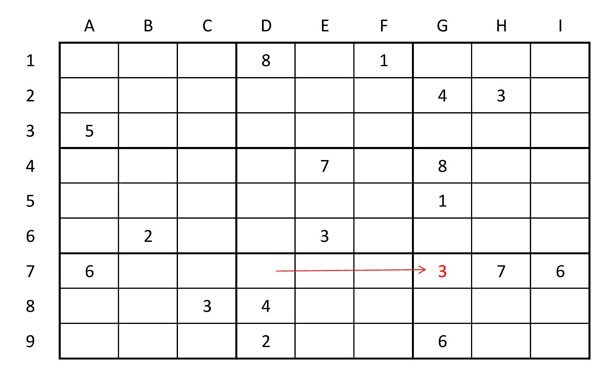
Determinarem estratègies que ens permetin eliminar números d’altres caselles. Per exemple , com que hi ha parelles dobles: A E4 i E5 (el 7 i 9), podrem eliminar tots els 7 i 9 de la resta de la columna (a E8 hi ha un 7). A E5 i H5 també hi ha un 7 i 9, o sigui podrem eliminar tots els de la resta de cel·les de la fila 5 (A5, B5, G5 i I5), i també tots els de la resta de cel·les de la seva regió (I4 i I6). A B5 i a I6 han quedat dos candidats únics (B5=1, I6=4)
Pas número 4
Eliminem números incompatibles
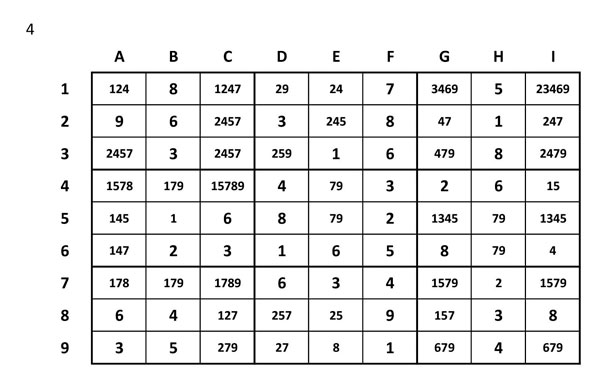
Ara escanejarem tots els grups d’acord amb com ha quedat. Per exemple a B5 hi ha l’1), i per tant alterarà tota la seva columna, la seva fila i la seva regió. També a I6 hi ha un candidat únic (el 4) i també altera la seva fila, la columna i la regió.
Pas número 5
Eliminar números incompatibles
Tornarem a modificar tots els grups d’acord amb aquests números únics.
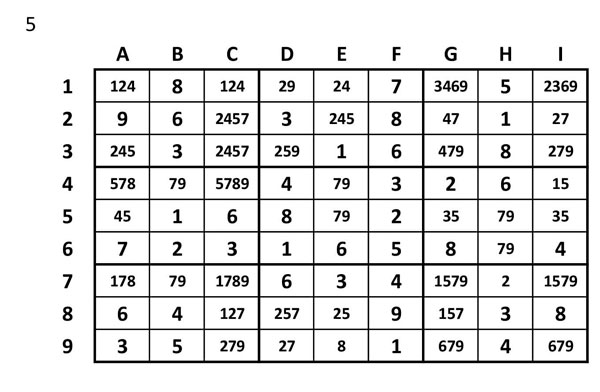
Pas número 6
Tornar a depurar
Haurem de tornar a modificar els grups d’acord amb aquest número únic (A6=7).
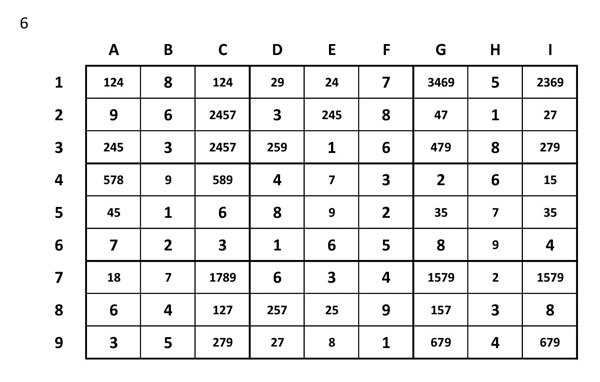
Pas número 7
Tornem a polir
Ara ja podem fer un escaneig de files, columnes i regions per veure si hi ha més números únics.
Com que a B7=7 podem eliminar tots els 7 de la regió i de la fila
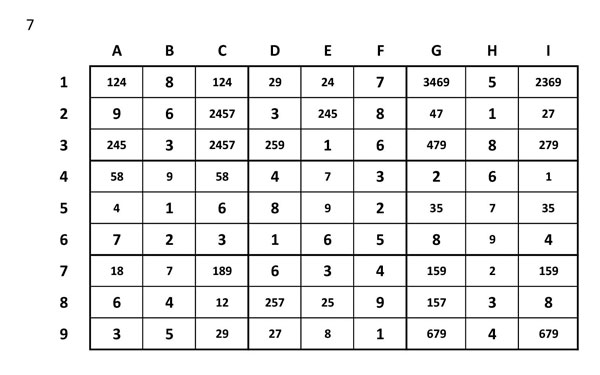
Pas número 8
Confirmar hipòtesis
Ara haurem d’escanejar línees, columnes i regions per trobar candidats únics.
A4=4 i per tant eliminem els altres de la columna (A1=12, A3=25)
Línea 7, només hi ha 5 a G7 i I7, per tant podem eliminar el de G8 (G8=17)
A la regió 7 només hi pot anar el 2 a la columna C: C8 i C9, per tant podem eliminar els de C1, C2 i C3
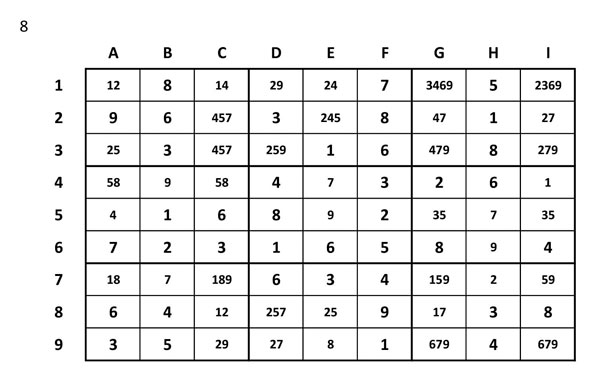
Pas número 9 – Hipòtesis arriscades (Nishio)
Regió 1. Casella A1=12
Si A1=2 –>I1 sense 2
Si A1=1 –> C1=4 –> E1=2 –> I1 sense 2
A la fila 1, el 4 no pot anar a G1, perquè si G1=4 –> E1=2 –> A1=1 –> C1=4 i no hi pot haver dos 4 a la mateixa fila.
Ara hem d’establir que D1=9 i eliminarem els 9 de G1 i H1. Partirem de la premissa que a la Columna D, els 7 només poden anar a la fila 8 i 9
Si D8=7 –>D9=2 –>D1=9
Si D9=7 –>C9=2 –>C8=1 –>C1=4 –>E1=2 –> D1=9
O sigui, que necessàriament D1=9 i eliminarem el 9 de G1 i de I1
Pas número 9
Situació límit
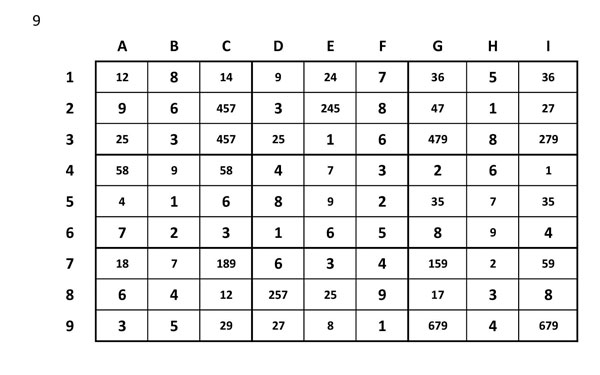
Pas número 10
Potser l’única opció
Ara arribem a una situació que sembla sense solució, però la clau està en que a la fila 9 només hi ha dues cel·les amb 2, a C9 i D9. Tan si va a un lloc com a l’altre, sempre elimina el 2 de E8.
Si D9=2 –> E8=5
Si C9=2 –>C9=1 –>C1=4 –>E1=2 –> E8=5
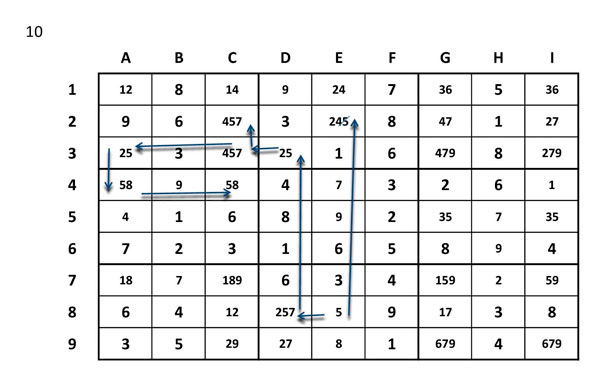
Pas número 11
Espigolada definitiva
I a partir d’aquí, amb E8=5 ja s’eliminen tots els altres en cadena fins arribar a l resultat de la figura 11